 11. Расчёт нанесённого урона в бою
11. Расчёт нанесённого урона в бою
(автор Монца, AlexSPl)
11.1 Общая формула для расчёта урона
Общая формула для расчёта урона, наносимого в бою, выглядит следующим образом:
| Damage = D*cnt*Hi |
| i = A1 — Z2 |
| Hi = (1.0 + 0.1*sign(i))**abs(i) |
| где: |
| D – урон атакующего юнита |
| cnt – количество атакующих юнитов |
| Hi — коэффициент урона |
| A1 – уровень атаки атакующего юнита, с учётом уровня атаки героя |
| Z2 — уровень защиты атакуемого юнита, с учётом уровня защиты героя |
| i — величина различия атаки атакующего и защиты атакуемого |
| sign(i) — функция знака числа. Если i < 0, то sign(i) = -1; если i = 0, то sign(i) = 0; если i > 0, то sign(i) = 1 |
| abs(i) — абсолютное значение. Если i < 0, то abs(i) = -i; иначе abs(i) = i |
| ** — возведение в степень |
Примечание — Значение D в большинстве случаев лежит в диапазоне от некого Dmin до Dmax.
Для точного определения нанесенного урона в бою, для любого атакуемого отряда под управлением игрока, необходимо во время боя воспользоваться программой LMOracle (См. раздел Программы и утилиты), либо использовать значения, приведённые в таблице:
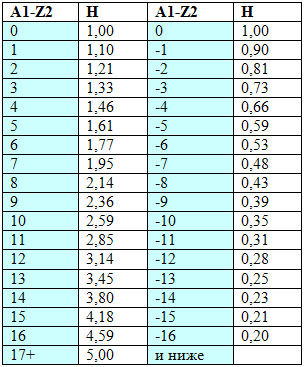
Нижеследующая форма позволит Вам рассчитать урон. Для этого необходимо просто заполнить её, подставив в активных полях нужные значения и выбрав монстров:
Как известно, минимальный урон в игре равен 1 HP, а вот максимальный урон, который может быть нанесён одним отрядом по одному стеку врага за одну атаку равен 32000 HP (даже джинны с их спецабилкой не могут снять более 32000 НР. Если 1 джинн атакует 500 драконов, и если сработает уполовинивание, то погибнет не 250 драконов, а всего только 160! (32000 / 200 = 160). Соответственно драконы, фениксы и циклопы за счёт умения атаковать на две клетки могут снять за одну атаку 64000 HP.
Если же говорить о максимальном уроне, который может нанести один отряд за один раунд, то безоговорочными лидерами будут гидры: под заклинанием «берсерк» за один удар они могут снять 32000 * 8 = 256000 HP, а если им придёт ещё и мораль после этого, то дополнительно 32000 * 5 = 160000 HP. Итого за один раунд — 416000 HP!
Примечание — гидры могут одновременно атаковать 8 стеков монстров на поле боя, если 3 дружественных стека монстров будут находиться под заклинанием «берсерк». На практике же (при игре), такую ситуацию встретить просто невозможно!
Примеры расчёта урона:
Пример 1: 100 крестьян атакуют огров. Уровень атаки крестьянина – 1. Урон крестьянина – 1. Уровень защиты огра – 5. Уровень атаки Героя – 13.
i = (1 + 13) — 5 = 9
H9 = (1.0 + 0.1)**9 = 2.36
Damage = 1 * 100 * 2.36 = 236
Пример 2: 100 крестьян атакуют дракона. Уровень атаки крестьянина – 1. Урон крестьянина – 1. Уровень защиты дракона – 12. Уровень атаки Героя – 1.
i = 12 — (1 + 1) = 10
H9 = (1.0 — 0.1)**10 = 0.35
Damage = 1 * 100 * 0.35 = 35
11.2 Вероятность выпадения конкретного урона
В Героях Меча и Магии I базовый урон генерируется отдельно для каждого воина в отряде.
В случае продолженной атаки (гидр, дыхание дракона, феникса, и т.д.) базовый урон для каждой цели рассчитывается отдельно (т.е. первый стек может получить 50 dmg, а второй — только 25 dmg). Кроме того, удвоение/уполовинивание урона в случае удачи/неудачи действует только для первой цели!
Пример 1. Пусть отряд состоит из 3-х драконов. Базовый урон есть сумма 3-х чисел из диапазона [25-50]. Например, базовый урон может составить 25 + 25 + 25 = 75, или 31 + 47 + 28 = 106, или 50 + 50 + 50 = 150 и т.д. Очевидно, что базовый урон 3-х драконов колеблется от 3*25 = 75 до 3*50 = 150.
Неискушённому игроку может показаться, что все уроны из диапазона [75-150] равновероятны, но это не так.
Пример 2. Три гнома ([2-4]) наносят базовый урон из диапазона [3*2-3*4] = [6-12], т.е. базовый урон трёх гномов может составлять 6, 7, 8, 9, 10, 11 или 12 ед. Рассмотрим все случаи:
| 1 гном | 2 гном | 3 гном | урон | 1 гном | 2 гном | 3 гном | урон | 1 гном | 2 гном | 3 гном | урон |
| 2 | 2 | 2 | 6 | 3 | 2 | 2 | 7 | 4 | 2 | 2 | 8 |
| 2 | 2 | 3 | 7 | 3 | 2 | 3 | 8 | 4 | 2 | 3 | 9 |
| 2 | 2 | 4 | 8 | 3 | 2 | 4 | 9 | 4 | 2 | 4 | 10 |
| 2 | 3 | 2 | 7 | 3 | 3 | 2 | 8 | 4 | 3 | 2 | 9 |
| 2 | 3 | 3 | 8 | 3 | 3 | 3 | 9 | 4 | 3 | 3 | 10 |
| 2 | 3 | 4 | 9 | 3 | 3 | 4 | 10 | 4 | 3 | 4 | 11 |
| 2 | 4 | 2 | 8 | 3 | 4 | 2 | 9 | 4 | 4 | 2 | 10 |
| 2 | 4 | 3 | 9 | 3 | 4 | 3 | 10 | 4 | 4 | 3 | 11 |
| 2 | 4 | 4 | 10 | 3 | 4 | 4 | 11 | 4 | 4 | 4 | 12 |
Всего возможных комбинаций n^k, где n — количество воинов в отряде, k — длина диапазона одного воина (количество возможных уронов). Для нашего случая n = 3, k = 4 — 2 + 1 = 3. Поэтому n^k = 3^3 = 27. Как видно, урон 6 может быть получен единственным способом (когда всем трём гномам генерируется урон 2), урон 7 может быть получен 3-мя способами и т.д.
- 6 — 1 способ (1 из 27, вероятность выпадения 1/27)
- 7 — 3 способа (3/27)
- 8 — 6 способов (6/27)
- 9 — 7 способов (7/27)
- 10 — 6 способов (6/27)
- 11 — 3 способа (3/27)
- 12 — 1 способ (1/27)
Таким образом, 3 гнома вероятнее всего нанесут 9 ед. урона (вероятность 7/27 = 25,9%). Вероятность нанести 6 или 12 ед. урона всего лишь 1/27 = 3,7%. В аддитивной теории чисел вышеприведённые разбиения (например, 10 = 2 + 4 + 4) называются композициями с M частями (для нашего случая M = 3), где каждая часть не превышает заданного числа N. Число таких композиций обозначается через c(N, M, n). Для с(N, M, n) существует формула. Здесь приводить не буду (не простая).
Т.о. вероятность выпадения конкретного урона = с(N, M, n)/n^k. Вероятность выпадения уронов на концах диапазона резко падает при увеличении числа воинов в отряде. Более вероятны уроны из центра диапазона. Теория отлично согласуется с практикой (распределение вероятностей выпадения уронов проверено тестерами).
Зачем это надо?
Для того, чтобы:
а) не удивляться, если Ваш отряд практически не наносит максимальный (или близкий к максимальному) урон;
б) удивляться, если это происходит у Вашего соперника;
Знание вероятностей выпадения урона также поможет оценке эффективности Ваших отрядов (типа какой лучше).
Все «случайные» числа в Героях Меча и Магии не совсем случайны, а именно псевдослучайны, поэтому все вероятности в игре следует принимать как ориентировочные. Любой ГПСЧ имеет период. Если он короткий, то псевдослучайные числа будут повторяться.
Примечание — Немного о том, насколько ГПСЧ Героев Меча и Магии I отличается от «идеального равномерного».
Будем рассматривать базовый урон base_dmg(Dragon) 1 (одного) дракона. Как известно, 25 <= base_dmg(Dragon) <= 50. Можно предположить, что все уроны из диапазона [25..50] равновероятны и вероятность выпадения любого урона из этого диапазона равна 1/(50 - 25 + 1) = 0,03846 (3,85%). Но ГПСЧ игры не идеален.
Реальные цифры приведены на рисунке ниже (не путать с вероятностями выпадения урона, когда существ в отряде больше одного).
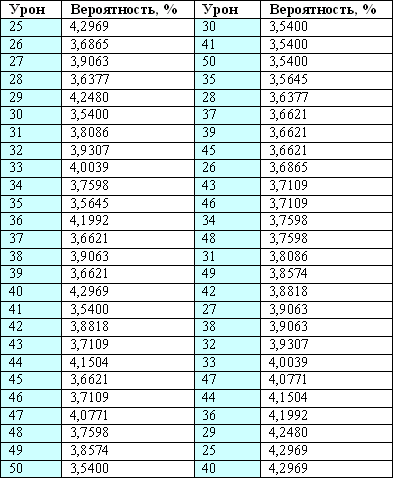
Благодаря неидеальности ГПСЧ дракон слегка перекошен в нижнюю половину уронов (25-37): 50,2442% . А идеальны в плане разброса вероятностей урона, например, монстры с уроном 1-2, 2-3, 2-5. Их уроны действительно равновероятны!
С ростом числа существ в отряде всё более вероятными становятся уроны из центра диапазона, всё менее вероятными — близ границ. Попробуйте, например, получить 20-ю драконами базовый урон 20*50 = 1000. Уверен, что у Вас вряд ли это получится. Подробнее про вычисление вероятности выпадения конкретного урона, в случае если отряд состоит более чем из одного монстра подробно описано выше.




а на вторых герое такой програмки нету?